Nov 4, 2024

Основы компиляции с использованием инкрементного подхода в python

Предисловие

Есть волшебный момент, когда программист нажимает кнопку «Запустить», и программное обеспечение начинает выполняться. Таким образом, программа, написанная на языке высокого уровня, работает на компьютере, который способен лишь перемещать биты. Здесь мы раскрываем волшебство, которое делает этот момент возможным. Начав с революционной работы Бэкуса и его коллег в 1950-х годах, ученые-компьютерщики разработали техники для создания программ под названием компиляторы, которые автоматически переводят программы высокого уровня в машинный код. Мы приглашаем вас в путешествие по созданию собственного компилятора для небольшого, но мощного языка. По пути мы объясняем основные концепции, алгоритмы и структуры данных, что лежат в основе компиляторов. Мы развиваем ваше понимание того, как программы отображаются на аппаратное обеспечение компьютера, что полезно для размышлений о свойствах на стыке аппаратного обеспечения и программного обеспечения, таких как время выполнения, программные ошибки и уязвимости безопасности. Для тех, кто заинтересован в карьере в области строительства компиляторов, наша цель — предоставить стартовую платформу для изучения таких сложных тем, как компиляция в реальном времени, анализ программ и оптимизация программ. Для тех, кто интересуется проектированием и реализацией языков программирования, мы связываем выбор дизайна языка с его воздействием на компилятор и сгенерированный код. Компилятор обычно организован как последовательность этапов, которые постепенно переводят программу в код, который выполняется на аппаратном обеспечении. Мы проводим этот подход до крайности, разбивая наш компилятор на множество нано-проходов, каждый из которых выполняет единственную задачу. Это позволяет тестировать каждый проход изолированно и сосредоточить наше внимание, делая компилятор значительно более понятным. Наиболее привычный подход к описанию компиляторов — это посвящение каждой главы одному проходу. Проблема этого подхода заключается в том, что он затемняет, как языковые особенности мотивируют дизайнерские решения в компиляторе. Вместо этого мы применяем инкрементальный подход, в котором мы создаем полный компилятор в каждой главе, начиная с небольшого входного языка, который включает только арифметику и переменные. Мы добавляем новые языковые особенности в последующих главах, при необходимости расширяя компилятор. Наш выбор языковых особенностей направлен на выявление основных концепций и алгоритмов, используемых в компиляторах.

• Мы начинаем с целочисленной арифметики и локальных переменных в главах 1 и 2, где мы вводим основные инструменты построения компилятора: абстрактные синтаксические деревья и рекурсивные функции.

• В главе 3 мы изучаем, как использовать фреймворк парсера Lark для создания парсера языка целочисленной арифметики и локальных переменных. Мы знакомимся с алгоритмами разбора, используемыми в Lark, включая Earley и LALR(1).

• В главе 4 мы применяем подсветку графов для назначения переменных машинным регистраторам.

• В главе 5 добавлены условные выражения, что мотивирует элегантный рекурсивный алгоритм для их преобразования в условные операторы goto.

• Глава 6 добавляет циклы. Это вызывает необходимость анализа потоков данных в регистровом аллокаторе.

• В главе 7 добавлены кортежи, распределенные по куче, что стимулирует сборщик мусора.

• Глава 8 добавляет функции как первоклассные значения без лексического объединения, подобно функциям в языке программирования C (Керниган и Ритчи, 1988). Читатель узнает о стеке вызовов процедур и соглашениях о вызовах, а также о том, как они взаимодействуют с выделением регистров и сборкой мусора. В главе также описывается, как генерировать эффективные хвостовые вызовы.

• Глава 9 добавляет анонимные функции с лексическим объединением, то есть лямбда-выражения. Читатель изучает преобразование замыканий, в котором лямбда-выражения переводятся в комбинацию функций и кортежей.

• Глава 10 добавляет динамическую типизацию. До этого момента входные языки были статически типизированными. Читатель расширяет статически типизированный язык с помощью типа Any, который служит целевым типом для компиляции динамически типизированного языка.

• Глава 11 использует тип Any, представленный в главе 10, для реализации постепенно типизированного языка, в котором различные области программы могут иметь как статическую, так и динамическую типизацию. Читатель реализует поддержку времени выполнения для прокси, которые позволяют безопасно перемещать значения между областями.

• Глава 12 добавляет дженерики с автоупаковкой, используя тип Any и приведения типов, разработанные в главах 10 и 11.

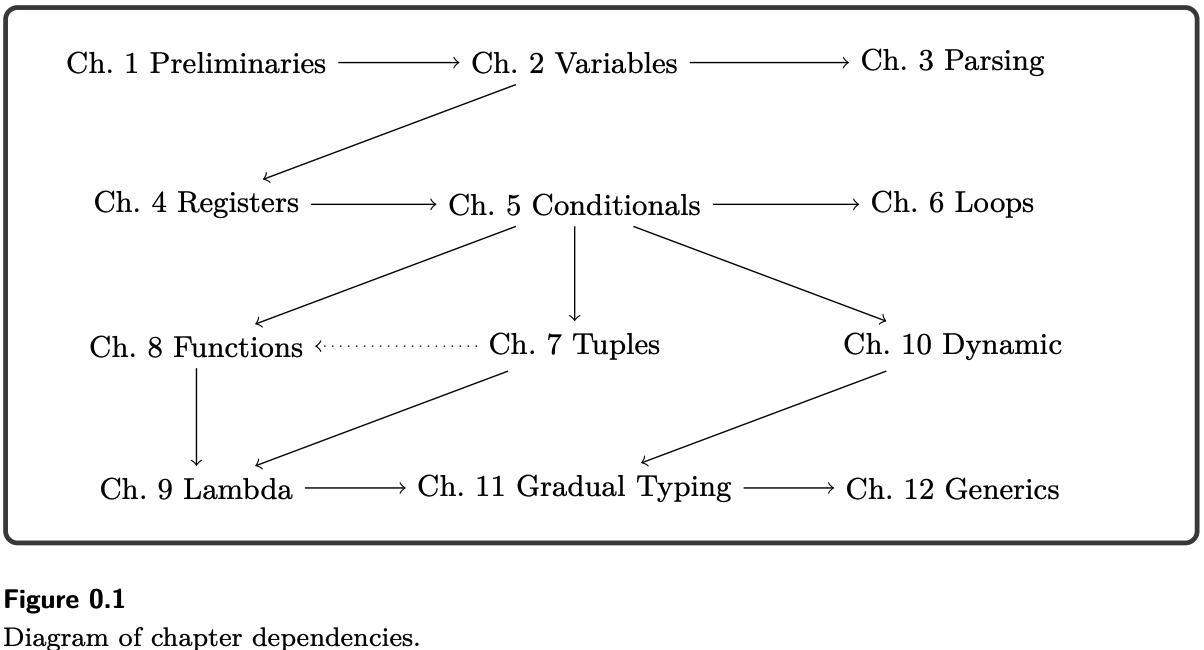
Существует множество языковых особенностей, которые мы не включаем. Наши выборы сбалансированы между случайной сложностью функции и основными концепциями, которые она раскрывает. Например, мы включаем кортежи, а не записи, потому что, хотя обе они побуждают изучение выделения в куче и сборки мусора, записи связаны с большей случайной сложностью. С 2009 года черновики этой книги служат учебником для шестнадцатинедельных курсов компиляторов для студентов старших курсов и аспирантов первого года в Университете Колорадо и Университете Индианы. Студенты приходят на курс с уже изученными основами программирования, структурами данных и алгоритмами, а также дискретной математикой. В начале курса студенты формируют группы из двух-четырех человек. Группы завершают примерно одну главу каждые две недели, начиная с главы 2 и включая главы в соответствии с интересами студентов, учитывая зависимости между главами, показанные на рисунке 0.1. Глава 8 (функции) зависит от главы 7 (кортежи) только в реализации эффективных хвостовых вызовов. Последние две недели курса предполагают финальный проект, в котором студенты разрабатывают и реализуют расширение компилятора по своему выбору. Последние главы могут быть использованы для поддержки этих проектов. Многие главы включают задачу с вызовом, которую мы назначаем аспирантам.

Для курсов компиляторов в университетах с квартальной системой (примерно десять недель) мы рекомендуем завершить курс до главы 7 или главы 8, предоставив студентам некоторый базовый код для каждого прохода компилятора. Курс можно адаптировать для акцента на функциональных языках, пропустив главу 6 (циклы) и включив главу 9 (лямбда). Курс можно адаптировать для динамически типизированных языков, добавив главу 10. Эта книга использовалась на курсах компиляторов в таких университетах, как Государственный университет Калифорнии в Политехническом институте, Университет штата Портленд, Институт технологии Роза-Халман, Университет Фрайбурга, Университет Массачусетса Лоуэлла и Университет Вермонта. В этом издании книги используется Python как для реализации компилятора, так и для входного языка, поэтому читатель должен быть хорошо знаком с Python. Существует множество отличных ресурсов для изучения Python (Lutz 2013; Barry 2016; Sweigart 2019; Matthes 2019). Код поддержки для этой книги находится в репозитории GitHub по следующему адресу: https://github.com/IUCompilerCourse/ Компилятор нацелен на ассемблерный язык x86 (Intel 2015), поэтому полезно, но не обязательно, чтобы читатель прошел курс по компьютерным системам (Bryant и O’Hallaron 2010). Мы вводим части ассемблерного языка x86-64, которые необходимы для компилятора. Мы следуем соглашениям о вызовах System V (Bryant и O’Hallaron 2005; Matz et al. 2013), поэтому сгенерированный ассемблерный код работает с системой времени выполнения (написанной на C), когда он компилируется с использованием компилятора GNU C (gcc) на операционных системах Linux и macOS на оборудовании Intel. На операционной системе Windows gcc использует соглашение о вызовах Microsoft x64 (Microsoft 2018, 2020). Поэтому сгенерированный ассемблерный код не работает с системой времени выполнения на Windows. Одним из обходных путей является использование виртуальной машины с Linux в качестве гостевой операционной системы.

Традиция создания компиляторов в Университете Индианы восходит к исследованиям и курсам по языкам программирования, проводимым Дэниелом Фридманом в 1970-х и 1980-х годах. Один из его студентов, Кент Дибвиг, реализовал Chez Scheme (Dybvig 2006), эффективный компилятор производственного качества для Scheme. В течение 1990-х и 2000-х годов Дибвиг преподавал курс компиляторов и продолжал разработку Chez Scheme. Курс компиляторов эволюционировал, чтобы включить новаторские педагогические идеи, а также элементы реальных компиляторов. Одной из идей Фридмана было разделение компилятора на множество небольших проходов. Другой идеей, называемой «игра», было тестирование кода, сгенерированного каждым проходом, с использованием интерпретаторов. Дибвиг, с помощью своих студентов Дипанвиты Саркара и Эндрю Кипа, разработал инфраструктуру для поддержки этого подхода и адаптировал курс для использования еще меньших нано-проходов (Sarkar, Waddell, и Dybvig 2004; Keep 2012). Многие из решений по проектированию компилятора в этой книге вдохновлены описаниями заданий Дибвига и Кипа (2010). В середине 2000-х годов один из студентов Дибвига по имени Абдулазиз Гулум заметил, что фронтально-обратная организация курса затрудняет понимание студентами логики проектирования компилятора. Гулум предложил инкрементальный подход (Ghuloum 2006), на котором основана эта книга. Я благодарю многих студентов, которые работали помощниками преподавателя на курсе компиляторов в ИУ, включая Карла Фактому, Райана Скотта, Кэмерона Свордса и Криса Уэйлса. Я благодарю Андре Куленшмидта за работу над сборщиком мусора и интерпретатором x86, Майкла Воллмера за работа над эффективными хвостовыми вызовами и Майкла Витоузека за помощь в первой реализации инкрементального курса компилятора в ИУ. Я благодарю профессоров Бор-Юх Чанга, Джона Климентса, Джея МаКартхи, Джозефа Нира, Райана Ньютона, Нейта Нистрома, Питера Тиеманна, Эндрю Толмача и Майкла Волловски за преподавание курсов на основе черновиков этой книги и за их отзывы. Я благодарю Национальный научный фонд за гранты, которые помогли поддержать эту работу: номера грантов 1518844, 1763922 и 1814460. Особая благодарность Рональду Гарсии за помощь в выживании на курсе компилятора Дибвига в начале 2000-х и за то, что он нашел баг, который заставил наш сборщик мусора гоняться за призраком!

Джереми Г. Сик
Блумингтон, Индиана

1 Введение.

В этой главе мы вводим основные инструменты, необходимые для реализации компилятора. Программы обычно вводятся программистом в виде текста, т.е. последовательности символов. Представление программы в виде текста называется конкретным синтаксисом. Мы используем конкретный синтаксис для краткой записи и обсуждения программ. Внутри компилятора мы используем абстрактные синтаксические деревья (AST) для представления программ таким образом, чтобы эффективно поддерживать операции, которые должен выполнять компилятор. Процесс перевода конкретного синтаксиса в абстрактный синтаксис называется разбором и изучается в главе 3. На данный момент мы используем функцию parse из модуля ast в Python для перевода от конкретного синтаксиса к абстрактному. AST можно представлять внутри компилятора различными способами в зависимости от используемого языка программирования. Мы используем классы и объекты Python для представления AST, особенно классы, определенные в стандартном модуле ast для языка Python. Мы используем грамматики для определения абстрактного синтаксиса языков программирования (раздел 1.2) и сопоставление с образцом, чтобы исследовать отдельные узлы в AST (раздел 1.3). Мы используем рекурсивные функции для построения и деконструирования AST (раздел 1.4). Эта глава предоставляет краткое введение в эти компоненты.

1.1 Абстрактные Синтаксические Деревья

Компиляторы используют абстрактные синтаксические деревья для представления программ, потому что они часто нуждаются в ответах на вопросы, такие как: для данной части программы, какой тип языковой особенности это? Каковы ее составные части? Рассмотрим программу слева и диаграмму её AST справа (1.1). Эта программа представляет собой операцию сложения, которая имеет две составные части: операцию ввода и отрицание. Отрицание имеет ещё одну составную часть — целочисленную константу 8. Используя дерево для представления программы, мы можем легко следовать по ссылкам, переходя от одной части программы к ее составным частям.

Мы используем стандартную терминологию для деревьев для описания абстрактных синтаксических деревьев (ASTs): каждый прямоугольник выше называется узлом(node). Стрелки соединяют узел с его дочерними(children) узлами, которые также являются узлами. Самый верхний узел называется корнем(root). Каждый узел, кроме корня, имеет родителя(parent) (узел, которому он является дочерним). Если узел не имеет дочерних узлов, он является листовым(leaf) узлом; в противном случае он является внутренним(internal) узлом. Мы используем класс Python для каждого типа узла. Ниже представлено определение класса для констант (также известных как литералы) из модуля ast Python.

class Constant:
    def __init__(self, value):
        self.value = value

Узел целочисленной константы содержит только одно значение — целочисленное значение. Чтобы создать узел AST для целого числа 8, мы пишем:

eight = Constant(8)

Мы говорим, что значение, созданное при помощи Constant(8), является экземпляром(instance) класса Constant. Следующее определение класса относится к унарным операторам.

class UnaryOp:
    def __init__(self, op, operand):
        self.op = op
        self.operand = operand

Конкретная операция указывается параметром op. Например, класс USub предназначен для унарного вычитания. (Больше унарных операторов будет представлено в следующих главах.) Чтобы создать AST, который представляет отрицание числа 8, мы пишем следующее:

neg_eight = UnaryOp(USub(), eight)

Вызов функции input_int представлен классами Call и Name.

class Call:
    def __init__(self, func, args):
        self.func = func
        self.args = args

class Name:
    def __init__(self, id):
        self.id = id

Чтобы создать узел AST, который вызывает input_int, мы пишем:

read = Call(Name('input_int'), [])

Наконец, для представления операции сложения в (1.1) мы используем класс BinOp для бинарных операторов.

class BinOp:
    def __init__(self, left, op, right):
        self.op = op
        self.left = left
        self.right = right

Теперь с помощью этих классов мы можем легко создавать и манипулировать абстрактными синтаксическими деревьями, представляя структуры программ в удобной для анализа форме. Подобно UnaryOp, конкретная операция определяется параметром op, который на данный момент представляет собой просто экземпляр класса Add. Таким образом, чтобы создать узел AST, который добавляет отрицательное восемь к какому-то пользовательскому вводу, мы пишем следующее:

ast1_1 = BinOp(read, Add(), neg_eight)

Чтобы компилировать программу, подобную (1.1), нам нужно знать, что операция, связанная с корневым узлом, — это сложение, и нам нужно иметь возможность получить доступ к его двум дочерним узлам. Python предоставляет сопоставление с образцом для поддержки таких запросов, как мы увидим в разделе 1.3. Мы часто записываем конкретный синтаксис программы, даже когда на самом деле имеем в виду AST, поскольку конкретный синтаксис более лаконичен. Мы рекомендуем вам всегда рассматривать программы как абстрактные синтаксические деревья.

1.2 Грамматики

Язык программирования можно рассматривать как множество(set) программ. Множество бесконечно (то есть всегда можно создавать более крупные программы), поэтому нельзя просто описать язык, перечислив все программы в нем. Вместо этого мы записываем набор правил, контекстно-свободную грамматику, для построения программ. Грамматики часто используются для определения конкретного синтаксиса языка, но также могут использоваться для описания абстрактного синтаксиса. Мы пишем наши правила в варианте формы Бэкуса-Наура (BNF) (Backus et al. 1960; Knuth 1964). В качестве примера мы описываем небольшой язык, названный $L_{Int}$ , который состоит из целых чисел и арифметических операций. Первое правило грамматики для абстрактного синтаксиса $L_{Int}$ говорит, что экземпляр класса Constant является выражением:

exp ::= Constant(int)

Каждое правило имеет левую и правую части. Если у вас есть узел AST, который соответствует правой части, то вы можете классифицировать его согласно левой части. Символы в шрифте наборного текста, такие как Constant, являются терминальными символами и должны буквально присутствовать в программе, чтобы правило применялось. Наши грамматики не упоминают пробелы, то есть разделители, такие как пробелы, табуляции и переносы строк. Пробелы могут быть вставлены между символами для устранения неоднозначности и улучшения читаемости. Имя, такое как exp, которое определяется правилами грамматики, называется нетерминальным. Имя int также является нетерминальным, но вместо того, чтобы определять его с помощью правила грамматики, мы определяем его следующим образом. Int — это последовательность десятичных цифр (от 0 до 9), возможно, начинающаяся с «–» (для отрицательных целых чисел), так что последовательность десятичных представляет целое число в диапазоне от –$2^{63}$ до $2^{63}$ – 1. Это позволяет представлять целые числа с использованием 64 бит, что упрощает несколько аспектов компиляции. В отличие от этого, целые числа в Python имеют неограниченную точность, но техники, необходимые для работы с неограниченной точностью, выходят за рамки данной книги.

Второе правило грамматики — это операция input_int, которая получает целое число на вход от пользователя программы:

exp ::= Call(Name('input_int'),[])

Третье правило классифицирует отрицание узла expr как expr.

exp ::= UnaryOp(USub(), exp) (1.4)

Мы можем применить эти правила для категоризации AST в языке $L_{Int}$ . Например, по правилу (1.2) Constant(8) является выражением exp, а затем по правилу (1.4) следующий AST также является выражением:

UnaryOp(USub(), Constant(8))

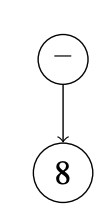(1.5)

Следующие два правила грамматики относятся к выражениям сложения и вычитания:

exp ::= BinOp(exp, Add(), exp) (1.6)
exp ::= BinOp(exp, Sub(), exp) (1.7)

Теперь мы можем обосновать, что AST (1.1) является выражением в $L_{Int}$. Мы знаем, что Call(Name('input_int'), []) является выражением по правилу (1.3), и мы уже классифицировали UnaryOp(USub(), Constant(8)) как exp, поэтому применяем правило (1.6), чтобы показать, что:

BinOp(Call(Name('input_int'), []), Add(), UnaryOp(USub(), Constant(8)))

является exp в языке $L_{Int}$.

Если у вас есть AST, для которого эти правила не применимы, то этот AST не принадлежит языку $L_{Int}$. Например, программа input_int() * 8 не находится в $L_{Int}$, потому что для оператора * нет правила. Всякий раз, когда мы определяем язык с помощью грамматики, язык включает только те программы, которые обоснованы правилами грамматики.

Язык $L_{Int}$ включает второй нетерминал stmt для операторов. Существует оператор для вывода значения выражения:

stmt ::= Expr(Call(Name('print'), [exp]))

и оператор, который вычисляет выражение, но игнорирует результат:

stmt ::= Expr(exp)

Последнее правило грамматики для $L_{Int}$ утверждает, что существует узел Module, который обозначает верхнюю часть всей программы:

LInt ::= Module(stmt∗)

Звёздочка * указывает на список предыдущего грамматического элемента, в данном случае — на список операторов. Класс Module определяется следующим образом:

class Module:
    def __init__(self, body):
        self.body = body

где body представляет собой список операторов.

exp ::= int | input_int() | - exp | exp + exp | exp - exp | (exp)
stmt ::= print(exp) | exp
LInt ::= stmt∗

Figure 1.1 Конкретный синтаксис языка $L_{Int}$.

exp ::= Constant(int) | Call(Name('input_int'),[]) 
       | UnaryOp(USub(), exp) | BinOp(exp, Add(), exp) 
       | BinOp(exp, Sub(), exp)
stmt ::= Expr(Call(Name('print'), [exp])) | Expr(exp)
LInt ::= Module(stmt∗)

Figure 1.1 Конкретный синтаксис языка $L_{Int}$.

Обычно бывает много правил грамматики с одной и той же левой частью, но с разными правыми частями, например, правила для exp в грамматике $L_{Int}$. В качестве сокращения можно использовать вертикальную палочку для комбинирования нескольких правых частей в одно правило. Конкретный синтаксис для $L_{Int}$ показан на рисунке 1.1, а абстрактный синтаксис для $L_{Int}$ показан на рисунке 1.2. Мы рекомендуем использовать функцию parse из модуля ast в Python для преобразования конкретного синтаксиса в абстрактное синтаксическое дерево.

1.3 Сопоставление с образцом

Как упоминалось в разделе 1.1, компиляторам часто необходимо получать доступ к частям узла AST. Начиная с версии 3.10, Python предоставляет возможность match для доступа к частям значения. Рассмотрим следующий пример:

match ast1_1:
    case BinOp(child1, op, child2):
        print(op)

В приведенном примере конструкция match проверяет, является ли AST (1.1) бинарным оператором и привязывает его части к трем переменным шаблона (child1, op и child2). В общем, каждый case состоит из шаблона и тела. Шаблоны рекурсивно определяются как одно из следующих: переменная шаблона, имя класса, за которым следует шаблон для каждого из аргументов его конструктора, или другие литералы, такие как строки или списки. Тело каждого case может содержать произвольный код на Python. Переменные шаблона могут использоваться в теле, например, op в строке print(op). Форма сопоставления (match) может содержать несколько пунктов, как в следующем примере функции leaf, которая распознает, когда узел $L_{Int}$ является листом в абстрактном синтаксическом дереве (AST). Сопоставление происходит по порядку, проверяя, соответствует ли шаблон входному AST. Код в первом совпадающем случае выполняется. Результаты вызова leaf для различных AST показаны справа:

def leaf(arith):
    match arith:
        case Constant(n):
            return True
        case Call(Name('input_int'), []):
            return True
        case UnaryOp(USub(), e1):
            return False
        case BinOp(e1, Add(), e2):
            return False
        case BinOp(e1, Sub(), e2):
            return False
            
print(leaf(Call(Name('input_int'), [])))  # True
print(leaf(UnaryOp(USub(), eight)))       # False
print(leaf(Constant(8)))                   # True

При создании выражения сопоставления мы обращаемся к определению грамматики, чтобы определить, какой нетерминал мы ожидаем сопоставить, и затем мы убеждаемся, что (1) у нас есть один случай для каждой альтернативы этого нетерминала и (2) шаблон в каждом случае соответствует правой части соответствующего правила грамматики. Для сопоставления в функции leaf мы обращаемся к грамматике $L_{Int}$, показанной на рисунке 1.2. Нетерминал exp имеет пять альтернатив, поэтому сопоставление содержит пять случаев. Шаблон в каждом случае соответствует правой части правила грамматики. Например, шаблон BinOp(e1, Add(), e2) соответствует правой части BinOp(exp, Add(), exp). При переводе из грамматик в шаблоны заменяем нетерминалы, такие как exp, на переменные шаблонов по вашему выбору (например, e1 и e2).

1.4 Рекурсивные Функции

Программы по своей природе рекурсивны. Например, выражение часто состоит из более мелких выражений. Поэтому естественный способ обработки всей программы — использовать рекурсивную функцию. В качестве первого примера такой рекурсивной функции мы определяем функцию is_exp, как показано на рисунке 1.3, чтобы принять произвольное значение и определить, является ли оно выражением в $L_{Int}$. Мы говорим, что функция определена с помощью структурной рекурсии, если она определяется с использованием последовательности случаев сопоставления, которые соответствуют грамматике, а тело каждого случая делает рекурсивный вызов для каждого дочернего $узла^1$.

Этот принцип структурирования кода в соответствии с определением данных поддерживается в книге «Как проектировать программы» (How to Design Programs) Фелайзена и др. (2001).

def is_exp(e):
    match e:
        case Constant(n):
            return True
        case Call(Name('input_int'), []):
            return True
        case UnaryOp(USub(), e1):
            return is_exp(e1)
        case BinOp(e1, Add(), e2):
            return is_exp(e1) and is_exp(e2)
        case BinOp(e1, Sub(), e2):
            return is_exp(e1) and is_exp(e2)
        case _:
            return False

def is_stmt(s):
    match s:
        case Expr(Call(Name('print'), [e])):
            return is_exp(e)
        case Expr(e):
            return is_exp(e)
        case _:
            return False

def is_Lint(p):
    match p:
        case Module(body):
            return all([is_stmt(s) for s in body])
        case _:
            return False

print(is_Lint(Module([Expr(ast1_1)])))
print(is_Lint(Module([Expr(BinOp(read, Sub(),
           UnaryOp(Add(), Constant(8))))])))

Рисунок 1.3 Пример рекурсивных функций для $L_{Int}$. Эти функции определяют, является ли AST частью $L_{Int}$. Мы определяем вторую функцию, названную is_stmt, которая распознает, является ли значение оператором $L_{Int}$ . Наконец, на рисунке 1.3 приведено определение функции is_Lint, которая определяет, является ли AST программой в $L_{Int}$. В общем, мы можем написать одну рекурсивную функцию для обработки каждого нетерминала в грамматике. Из двух примеров внизу рисунка первый относится к $L_{Int}$ , а второй — нет.

1.5 Интерпретаторы

Поведение программы определяется спецификацией языка программирования. Например, язык Python определен в справочнике по языку Python (Python Software Foundation 2021b) и интерпретаторе CPython (Python Software Foundation 2021a). В этой книге мы используем интерпретаторы для спецификации каждого языка, который рассматриваем. Интерпретатор, который обозначается как определение языка, называется определяющим интерпретатором (Reynolds 1972). Мы начнем с создания определяющего интерпретатора для языка $L_{Int}$. Этот интерпретатор служит вторым примером структурной рекурсии. Определение функции interp_Lint показано на рисунке 1.4. Тело функции сопоставляет с AST-узлом Module и затем вызывает interp_stmt для каждого оператора в модуле. Функция interp_stmt включает случай для каждого правила грамматики нетерминала stmt и вызывает interp_exp для каждого подвыражения. Функция interp_exp включает случай для каждого правила грамматики нетерминала exp. Мы используем несколько вспомогательных функций, таких как add64 и input_int, которые определены в коде поддержки этой книги. Рассмотрим результат интерпретации нескольких программ на $L_{Int}$ . Следующая программа складывает два целых числа:

print(10 + 32)

Результат — 42, ответ на вопрос о жизни, вселенной и обо всем: $42!^2$

The Hitchhiker’s Guide to the Galaxy by Douglas Adams.

Мы написали эту программу в конкретном синтаксисе, в то время как разобранный абстрактный синтаксис выглядит так:

Module([Expr(Call(Name('print'), [BinOp(Constant(10), Add(), Constant(32))]))])

Следующая программа демонстрирует, что выражения могут быть вложены друг в друга, в данном случае — несколько сложений и отрицаний.

print(10 + -(12 + 20))

Каков результат этой программы? Последней особенностью языка $L_{Int}$ является операция input_int, которая запрашивает у пользователя программу целое число. Напомним, что программа (1.1) запрашивает ввод целого числа, а затем вычитает 8. Итак, если мы запустим

interp_Lint(Module([Expr(Call(Name('print'), [ast1_1]))]))

и если ввод равен 50, результат будет 42. Мы включили операцию input_int в $L_{Int}$, чтобы изобретательный студент не смог реализовать компилятор для $L_{Int}$, который просто выполняет интерпретатор во время компиляции, чтобы получить вывод, а затем сгенерировать тривиальный код для его $получения^3$.

Да, один умный студент сделал это в первом выпуске этого курса!

Задача компилятора состоит в том, чтобы перевести программу на одном языке в программу на другом языке так, чтобы выходная программа вело себя так же, как входная программа. Эта идея изображена на следующей диаграмме.

def interp_exp(e):
    match e:
        case BinOp(left, Add(), right):
            l = interp_exp(left); r = interp_exp(right)
            return add64(l, r)
        case BinOp(left, Sub(), right):
            l = interp_exp(left); r = interp_exp(right)
            return sub64(l, r)
        case UnaryOp(USub(), v):
            return neg64(interp_exp(v))
        case Constant(value):
            return value
        case Call(Name('input_int'), []):
            return input_int()

def interp_stmt(s):
    match s:
        case Expr(Call(Name('print'), [arg])):
            print(interp_exp(arg))
        case Expr(value):
            interp_exp(value)

def interp_Lint(p):
    match p:
        case Module(body):
            for s in body:
                interp_stmt(s)

Предположим, что у нас есть два языка, $L_1$ и $L_2$ , и определяющий интерпретатор для каждого языка. Учитывая компилятор, который переводит язык $L_1$ в язык $L_2$, и любую программу $P_1$ на $L_1$, компилятор должен перевести её в некоторую программу $P_2$ таким образом, чтобы интерпретация $P_1$ и $P_2$ на своих интерпретаторах с одинаковым вводом i давала одинаковый вывод o.

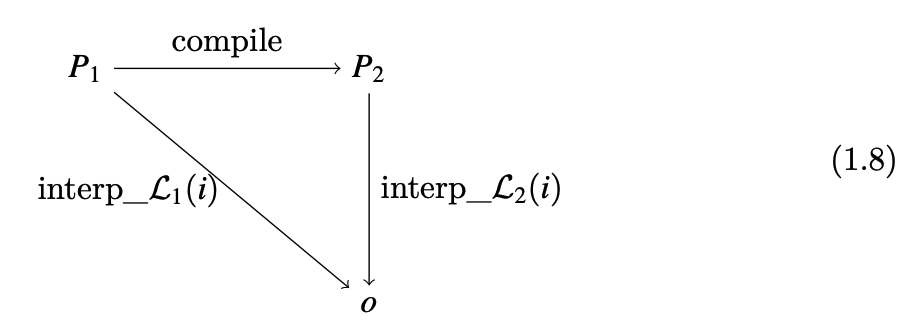
Мы устанавливаем условие, что если выполнение определяющего интерпретатора программы вызывает ошибку, то значение этой программы не определено, если только поднятое исключение не является TrappedError. Компилятор для данного языка не несет обязательств относительно программ с неопределенным поведением; он не обязан производить исполняемый файл, и если он это делает, то этот исполняемый файл может выполнять любые действия. С другой стороны, если ошибка является TrappedError, компилятор обязан создать исполняемый файл и сообщить о том, что произошла ошибка. Для сигнала об ошибке необходимо выйти с кодом возврата 255. Интерпретаторы в главах 10 и 11, а также в разделе 7.9 используют TrappedError.

1.6 Пример компилятора: частичный интерпретатор

В этом разделе мы рассматриваем компилятор, который переводит программы $L_{Int}$ в более эффективные программы $L_{Int}$. Компилятор с жадным подходом вычисляет части программы, которые не зависят от входных данных, процесс, известный как частичная оценка (Jones, Gomard и Sestoft 1993). Например, для следующей программы:

print(input_int() + -(5 + 3))

наш компилятор переводит её в программу:

print(input_int() + -8)

Рисунок 1.5 показывает код простого частичного вычислителя для языка $L_{Int}$ . Выходные данные частичного вычислителя — эта же программа, написанная на $L_{Int}$ . В рисунке 1.5 структурная рекурсия по выражению захватывается в функции pe_exp, в то время как код для частичной оценки операций отрицания и сложения разделен на три вспомогательные функции: pe_neg, pe_add и pe_sub. Входными данными для этих функций является результат частичной оценки их дочерних узлов. Функции pe_neg, pe_add и pe_sub проверяют, являются ли их аргументы целыми числами, и если да, то выполняют соответствующие арифметические операции. В противном случае они создают узел AST для арифметической операции. Чтобы убедиться, что частичный вычислитель работает правильно, мы можем проверить, производит ли он программы, которые дают такой же результат, как и исходные программы. То есть мы можем проверить, соответствует ли он диаграмме (1.8).

Упражнение 1.1: Создайте три программы на языке $L_{Int}$ и проверьте, дает ли частичная оценка с помощью pe_Lint, а затем интерпретация с помощью interp_Lint тот же результат, что и прямая интерпретация с помощью interp_Lint.

def pe_neg(r):
    match r:
        case Constant(n):
            return Constant(neg64(n))
        case _:
            return UnaryOp(USub(), r)

def pe_add(r1, r2):
    match (r1, r2):
        case (Constant(n1), Constant(n2)):
            return Constant(add64(n1, n2))
        case _:
            return BinOp(r1, Add(), r2)

def pe_sub(r1, r2):
    match (r1, r2):
        case (Constant(n1), Constant(n2)):
            return Constant(sub64(n1, n2))
        case _:
            return BinOp(r1, Sub(), r2)

def pe_exp(e):
    match e:
        case BinOp(left, Add(), right):
            return pe_add(pe_exp(left), pe_exp(right))
        case BinOp(left, Sub(), right):
            return pe_sub(pe_exp(left), pe_exp(right))
        case UnaryOp(USub(), v):
            return pe_neg(pe_exp(v))
        case Constant(value):
            return e
        case Call(Name('input_int'), []):
            return e

def pe_stmt(s):
    match s:
        case Expr(Call(Name('print'), [arg])):
            return Expr(Call(Name('print'), [pe_exp(arg)]))
        case Expr(value):
            return Expr(pe_exp(value))

def pe_P_int(p):
    match p:
        case Module(body):
            new_body = [pe_stmt(s) for s in body]
            return Module(new_body)

Figure 1.5 Частичный вычислитель для $L_{Int}$.